Tópicos em Métodos Quantitativos
Se você já entende bem o conceito de derivadas e taxas de crescimento, vamos agora então revisar alguns conceitos de logaritmos e aplica-los nessas mesmas taxas. Caso você ainda não tenha muito claro estes primeiros conceitos, clique aqui.
Basicamente, as propriedades de logaritmos que você mais deverá usar são as seguintes:

É interessante ainda lembrar que, para o logaritmo natural, ln(1) = 0 e ln(e) = 0. (Caso você não conheça a definição de logaritmo natural clique aqui).
Se um dia qualquer você se deparar com uma função do tipo y(t) = log x(t), poderá fazer a seguinte derivação:
.bmp)
Ou seja, poderá ver que, se uma variável (digamos y) for função de uma outra variável (digamos x) que existe em função do tempo, poderemos usar a regra da cadeia (caso desconheça ou não se lembre da regra da cadeia, clique aqui), e dessa forma, concluir que:
A DERIVADA EM RELAÇÃO AO TEMPO DO LOGARITMO DE UMA VARIÁVEL É A TAXA DE CRESCIMENTO DA VARIÁVEL
Ou seja, na função acima, a derivada em relação ao tempo do log de x é a taxa de crescimento de x. Dessa forma, se pudermos expressar a relação de alguma coisa com o tempo em forma de logaritmo, teremos então instantaneamente a sua taxa de crescimento através da derivada. Caso você continue os seus estudos nessa área, verá que isto é bastante importante para se compreender vários fenômenos em diversas ciências.
Se por exemplo, tomarmos uma função do tipo Cobb-Douglas, muito comum para expressar funções de produção de firmas, teríamos como torná-la linear fazendo os seguintes ajustes:
Tomamos a função e aplicamos o logaritmo em ambos os lados:

Como, pelo o que vimos nas propriedades, o logaritmo do produto é igual a soma dos logaritmos (log xy = log x + log y), podemos dizer que:

Agora, se quisermos observar a taxa de crescimento de Y em relação ao tempo, podemos derivar a função em relação ao tempo:

E como observamos anteriormente que a derivada do logaritmo de uma variável em relação ao tempo é igual à taxa de crescimento da variável, chegamos à seguinte identidade:

Assim, se a função de produção de uma firma for do tipo Cobb-Douglas, podemos dizer que a taxa de crescimento do seu produto será igual à média das taxas de crescimento dos seus insumos ponderada pelas elasticidades do produto em relação à cada fator¹. Além do que, podemos ainda colocar que a elasticidade de duas grandezas pode ser tirada na seguinte forma:

Que simplesmente resulta do fato de que a variação absoluta do logaritmo de uma variável (dlogx) é a variação percentual dessa variável, e no caso da variação temporal dt for igual a um, teremos que

Podemos supor ainda uma outra condição comum ao mundo real... a condição na qual uma determinada variável apresente crescimento exponencial, na qual, se aplicarmos as propriedades que já anunciamos no início desse texto, teremos:

Bom, e qual é a importância desse resultado?
Basicamente ele nos permite calcular a taxa de crescimento entre dois períodos t e t - 1 (algo extremamente importante para avaliarmos fenômenos temporais). Se tomarmos y0 como y(t - 1), e tomarmos t = 1 (afinal saímos de y0), podemos então definir g como:
.bmp)
Uma vez que se tomarmos:

Como temos que Ln(exponencial de g) é igual a g e Ln(1) é igual a zero, temos que a taxa de crescimento é g.
1. A elasticidade, ou seja a sensibilidade do produto em relação à K (que podemos definir como capital), é dada pela variação do produto para cada variação em K, e comumente esta variação é tomada em porcentagem para evitar confusões de medidas. Então, para o caso de uma Cobb-Douglas temos:

E a mesma lógica se aplica à elasticidade de Y em relação a L.


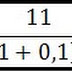


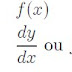


Parabéns! Muito bom o artigo, me ajudou muito!
ResponderExcluirmuito bom!
ResponderExcluirdafabet link dafabet link 12bet 12bet starvegad starvegad 온카지노 온카지노 1xbet korean 1xbet korean fun88 fun88 dafabet dafabet bet365 bet365 카지노사이트 카지노사이트 623
ResponderExcluir